Árboles de Análisis Abstracto
Un Árbol de Análisis Abstracto (denotado AAA, en inglés AST) porta la misma información que el árbol de análisis sintáctico concreto pero de forma mas condensada, eliminándose terminales y producciones que no aportan información.
The data structure that the parser will use to describe a program consists of node objects, each of which has a type property indicating the kind of expression it is and other properties to describe its content.
El árbol de análisis sintáctico abstracto es una representación compactada del árbol de análisis sintáctico concreto que contiene la misma información que éste.
Por ejemplo, para una gramática que acepta expresiones como:
x=1
y=2
3*(x+y)
este es un ejemplo de árbol sintáctico concreto:
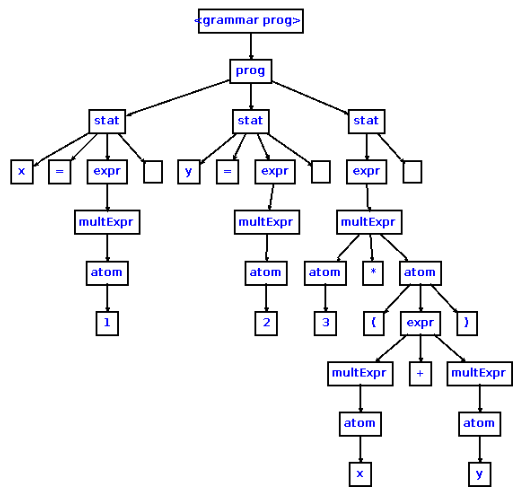
y este un posible árbol sintáctico abstracto con la misma información que el anterior:
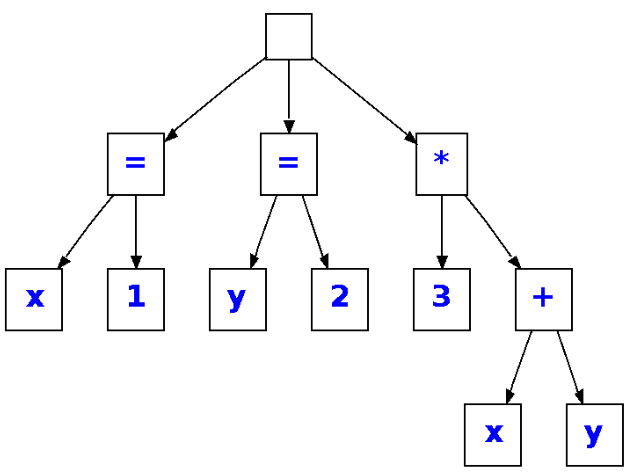
Alfabeto con Aridad o Alfabeto Árbol
No deja de ser curioso que es posible definir un equivalente del cierre de Kleene \(\Sigma^*\) de un alfabeto \(\Sigma\) para modelizar matemáticamente los árboles.
Para ello se empieza definiendo lo que es un alfabeto con función de aridad:
Alfabeto con Función de Aridad
Un alfabeto con función de aridad es un par \((\Sigma, \rho)\) donde \(\Sigma\) es un conjunto finito y \(\rho\) es una función
\[\rho: \Sigma \rightarrow ℕ_0 \cup \{ * \}\]denominada función de aridad. Aquí \(ℕ_0\) denota al conjunto de los números naturales incluyendo el cero.
Denotamos por \(\Sigma_k\) los elementos del alfabeto con aridad k:
\[\Sigma_k = \{ a \in \Sigma :\ \rho(a) = k \}\]\(\Sigma_0\) son las hojas, \(\Sigma_1\) son los elementos con un solo hijo, \(\Sigma_2\) los nodos binarios, \(\Sigma_*\) son los nodos con aridad variable, etc.
Lenguaje de los Arboles o Términos
Definimos el conjunto de los árboles \(B(\Sigma)\) con alfabeto \(\Sigma\) inductivamente:
- El árbol vacío está en \(B(\Sigma)\)
- Todos los elementos de aridad 0 así como los de aridad variable \(\Sigma_*\) están en \(B(\Sigma)\):
- \(a \in \Sigma_0\) implica \(a \in B(\Sigma)\)
- \(a \in \Sigma_*\) implica \(a \in B(\Sigma)\)
- Si \(b_1, \ldots , b_k \in B(\Sigma)\) y \(f \in \Sigma_k\) es un elemento \(k\)-ario o bien es de aridad variable, entonces \(f(b_1 \ldots b_k) \in B(\Sigma)\)
Los elementos de \(B(\Sigma)\) se llaman árboles o términos.
\(B(\Sigma)\) es el conjunto de todos los árboles posibles.
Al igual que cuando parseamos las cadenas hablamos de tokens para hablar de la ocurrencia en la cadena de un elemento del alfabeto aquí hablamos de nodos para hablar de la ocurrencia de un elemento \(f \in \Sigma_k\) dentro de un árbol.
\(B(\Sigma)\) es a los nodos (árboles) lo que \(\Sigma*\) es a las tokens (strings).
Aridad de los Nodos en Egg
Los AST con los que trabajamos en nuestro parser son de tres tipos
\[\Sigma = \{ VALUE, \, WORD, \, APPLY, \, ARRAY \}\]con aridad:
- \(\rho(VALUE) = 0\) los nodos VALUE son hojas
- \(\rho(WORD) = 0\) los nodos WORD los consideramos hojas
- \(\rho(APPLY) = 2\) un APPLY tiene dos hijos: el hijo OPERATOR y el hijo ARGS que es un array
- \(\rho(ARRAY) = *\) los arrays contienen diferentes números de árboles
Implementación de los Nodos de los AST de Egg
En cuanto a la implementación, al igual que con los tokens, los nodos son objetos y tienen propiedades.
Todos los nodos tiene una propiedad type que determina que tipo de nodo es y por tanto su aridad.
- Los nodos del tipo
VALUErepresentan constantes (literals) STRINGS o NUMBERS.- Their
valueproperty contains the string or number value that they represent.
- Their
- Nodes of type
WORDare used for identifiers (names).- Such objects have a
nameproperty that holds the identifier’s name as a string.
- Such objects have a
APPLYnodes represent applications. They have anoperatorproperty that refers to the expression that is being applied, and anargsproperty that is an special node:ARRAY
ARRAYis in fact an special node of ASTs that holds the arguments of the application
Example: AST >(x, 5)
For example, The AST resulting from parsing the input
>(x, 5)
would be represented like this term:
APPLY(
WORD,
ARRAY[
WORD,
VALUE
]
)
or if we want to explicit the attributes we can extend the notation to look like this:
APPLY(
operator: WORD{name:>},
args: ARRAY[
WORD{name:x}
VALUE{value:5}
]
)
More precisely, describing its actual implementation attributes:
$ cat greater-x-5.egg
>(x,5)
$ ./eggc.js greater-x-5.egg
$ cat greater-x-5.egg.evm
Here is the JSON:
{
"type": "apply",
"operator": {
"type": "word",
"name": ">"
},
"args": [
{
"type": "word",
"name": "x"
},
{
"type": "value",
"value": 5
}
]
}
Example: AST ` +(a,*(4,5))`
Otro ejemplo, el AST para +(a,*(4,5)) sería
APPLY(
WORD,
ARRAY[
WORD,
APPLY(
WORD,
ARRAY[VALUE, VALUE]
)
]
)
Que explicitando los atributos sería:
APPLY(
operator: WORD[{name: +},
args: ARRAY[
WORD{name: a},
APPLY(
name: WORD{name:*},
args: ARRAY[VALUE{value:4}, VALUE{value:5}]
)
]
)
Gramática Árbol
Una Gramática Árbol en nuestra definición es una cuadrupla \(((\Sigma, \rho), N, P, S)\), donde:
-
\((\Sigma, \rho)\) es un alfabeto con aridad \(\rho: \Sigma \rightarrow ℕ_0 \cup \{ * \}\)
-
\(N\) es un conjunto finito de variables sintácticas o no terminales
-
\(P\) es un conjunto finito de reglas de producción de la forma \(A \rightarrow s\) con \(A \in N\) y \(s \in B(\Sigma \cup N)\)
-
\(S \in N\) es la variable o símbolo de arranque
NOTA: Regular Tree Grammar en la Wikipedia
Gramática Informal de los árboles del Parser de Egg
En nuestro intérprete de Egg los árboles usados son los generados por esta gramática:
ast: VALUE
| WORD
| APPLY( WORD ARRAY( ast * ))
Notación de Dewey o Coordenadas de un Árbol
La notación de Dewey (1876) es una forma de especificar los subárboles de un árbol \(t \in B(\Sigma)\). La notación sigue el mismo esquema que la numeración de secciones en un texto: es una palabra formada por números separados por puntos. Así t/2.1.3 denota al tercer hijo del primer hijo del segundo hijo del árbol \(t\).
La definición formal por inducción sería:
-
\(t/\epsilon = t\). Esto es, si el sufijo es \(\epsilon\) es el propio árbol
-
Si \(t = a(t_1, \ldots t_k)\) y \(j \in \{ 1 \ldots k \}\) y \(n\) es una cadena de números y puntos, se define inductivamente el subárbol \(t/j.n\) como el subárbol \(n\)-ésimo del \(j\)-ésimo subárbol de \(t\). Esto es: \(t/j.n = t_j/n\)
Por ejemplo si:
t =
APPLY(
operator: WORD{name:+},
args: [
WORD{name:a},
APPLY(
operator: WORD{name:*},
args: [VALUE{value:4},VALUE{value:5}]
)
]
)
Entonces (indexando en 1), si no me equivoco:
- t/1 sería el árbol WORD{name:+}
- t/2.1 sería el WORD{name:a}
- t/2.2.2.1 sería *VALUE{value:4}
Es una idea muy repetida: Otras notaciones
En realidad, la notación de Dewey es equivalente al operador “.”
que usamos en los lenguajes de programación para denotar los atributos de un objeto.
Con el “.” a partir de t podemos construir expresiones como:
t.operator, t.operator.name, t.args.0.name, t.args.1.args.0.value
La misma idea aparece en el uso del operador “/” para denotar subdirectorios en Unix
/src/js/tutu.js y sub-recursos en una URL.
También en el lenguaje XPath para hablar de elementos de los objetos de un documento XML.
For example, the expression “A//B/*[1]” selects the first child (“*[1]”), whatever its name, of every “B” element that itself is a child or other, deeper descendant (“//”) of an “A” element that is a child of the current context node (the expression does not begin with a “/”).
The language jq to select sub-objects inside a JSON is another example.
Códigos para la Construcción de los ASTs de Egg con un algoritmo PDR
Código de parse
function parse(p) {
setProgram(p);
lex();
let result = parseExpression();
if (lookahead !== null)
throw new SyntaxError(`Unexpected input after reached the end of parsing ${lineno}: ${program.slice(0,10)}`);
return result;
}
Código de parseExpression
function parseExpression() {
let expr;
if (lookahead.type == "STRING") {
expr = {type: "value", value: lookahead.value};
lex();
return expr;
} else if (lookahead.type == "NUMBER") {
expr = {type: "value", value: lookahead.value};
lex();
return expr;
} else if (lookahead.type == "WORD") {
expr = {type: "word", name: lookahead.value};
lex();
return parseApply(expr);
} else {
throw new SyntaxError(`Unexpected syntax line ${lineno}: ${program.slice(0,10)}`);
}
}
Código de parseApply
function parseApply(tree) {
if (!lookahead) return tree; // apply: /* vacio */
if (lookahead.type !== "LP") return tree; // apply: /* vacio */
lex();
tree = {type: 'apply', operator: tree, args: []};
while (lookahead && lookahead.type !== "RP") {
let arg = parseExpression();
tree.args.push(arg);
if (lookahead && lookahead.type == "COMMA") {
lex();
} else if (!lookahead || lookahead.type !== "RP") {
throw new SyntaxError(`Expected ',' or ')' at line ${lineno}: ... ${program.slice(0,20)}`);
}
}
if (!lookahead) throw new SyntaxError(`Expected ')' at line ${lineno}: ... ${program.slice(0,20)}`);
lex();
return parseApply(tree);
}